Dana jest prostokątna plansza złożona z n wierszy i m kolumn zawierająca n * m pól.
Wiersze są ponumerowane od góry kolejnymi liczbami 1, 2, …, n,
natomiast kolumny od lewej do prawej kolejnymi liczbami 1, 2, …, m.
Każde pole jest albo białe, albo czarne.
Planszę możemy opisać jako tablicę dwuwymiarową A[1..n][1..m], w której A[ i ][ j ] = 0 jeśli pole w i-tym wierszu i j-tej kolumnie jest czarne,
natomiast A[ i ][ j ] = 1, jeśli to pole jest białe.
Pola w lewym górnym rogu oraz prawym dolnym rogu zawsze są białe (czyli A[1][1] = 1 oraz A[n][m] = 1).
Rozważmy następujący algorytm, w którym jest wykorzystywana pomocnicza tablica P[1..n][1..m], przyjmująca wartości logiczne (PRAWDA albo FAŁSZ).
Specyfikacja:
Dane: n, m – liczby całkowite dodatnie, wymiary planszy, A[1..n][1..m] – opis planszy
Wynik: PRAWDA albo FAŁSZ
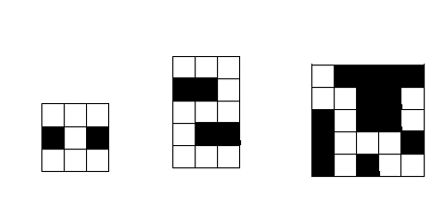
Podaj wynik działania algorytmu dla plansz podanych na rysunkach poniżej.
24_11.jpg cennik.txt jablka.txt kierowcy.txt liczby.txt rejestr.txt skrot.txt skrot2.txt taryfikator.txt
Wiersze są ponumerowane od góry kolejnymi liczbami 1, 2, …, n,
natomiast kolumny od lewej do prawej kolejnymi liczbami 1, 2, …, m.
Każde pole jest albo białe, albo czarne.
Planszę możemy opisać jako tablicę dwuwymiarową A[1..n][1..m], w której A[ i ][ j ] = 0 jeśli pole w i-tym wierszu i j-tej kolumnie jest czarne,
natomiast A[ i ][ j ] = 1, jeśli to pole jest białe.
Pola w lewym górnym rogu oraz prawym dolnym rogu zawsze są białe (czyli A[1][1] = 1 oraz A[n][m] = 1).
Rozważmy następujący algorytm, w którym jest wykorzystywana pomocnicza tablica P[1..n][1..m], przyjmująca wartości logiczne (PRAWDA albo FAŁSZ).
Specyfikacja:
Dane: n, m – liczby całkowite dodatnie, wymiary planszy, A[1..n][1..m] – opis planszy
Wynik: PRAWDA albo FAŁSZ
P[1][1] ← PRAWDA
dla i = 1, 2, ..., n wykonuj
dla j = 1, 2, .., m wykonuj
jeżeli A[ i ][ j ] = 0: P[ i ][ j ] ← FAŁSZ
w przeciwnym przypadku
jeżeli i = 1 oraz j ≠ 1: P[ i ][ j ] ← P[ i ][ j – 1 ]
jeżeli i ≠ 1 oraz j = 1: P[ i ][ j ] ← P[ i – 1 ][ j ]
jeżeli i ≠ 1 oraz j ≠ 1: P[ i ][ j ] ← P[ i ][ j – 1 ] lub P[ i – 1 ][ j ]
podaj wynik P[n][m]
Podaj wynik działania algorytmu dla plansz podanych na rysunkach poniżej.
