Następujący rekurencyjny algorytm mnożenia dwóch liczb całkowitych dodatnich x, y jest realizowany z użyciem operacji arytmetycznych dodawania i dzielenia całkowitego przez 2.
Uwaga: x mod y oznacza resztę z dzielenia x przez y, natomiast x div y oznacza wynik dzielenia całkowitego x przez y.
Dla danych liczb x, y interesuje nas liczba wykonywanych operacji dodawania podczas obliczania wyniku funkcji iloczyn(x, y).
Przykład 1.
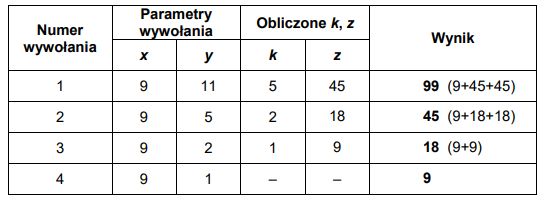
Dla liczb x=9 i y=11 algorytm wykonuje 5 dodawań. Działanie funkcji iloczyn(9, 11) można zilustrować w następujący sposób (w nawiasach obok wskazano liczbę wykonywanych operacji dodawania):
iloczyn(9, 11) = 9 + z + z, (dwa dodawania) gdzie z = iloczyn(9, 5)
iloczyn(9, 5) = 9 + z + z, (dwa dodawania) gdzie z = iloczyn(9, 2)
iloczyn(9, 2) = z + z, (jedno dodawanie) gdzie z = iloczyn(9, 1)
iloczyn(9, 1) = 9
Uzupełnij poniższą tabelę tak, aby ilustrowała obliczenia wykonywane podczas wywołania iloczyn(10, 45)
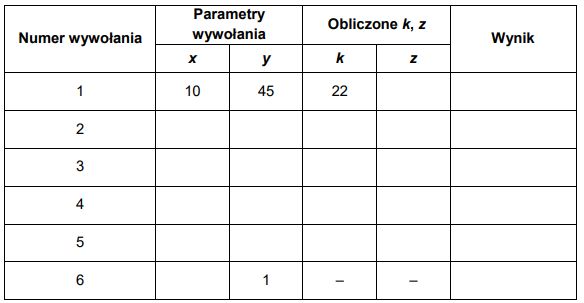
W odpowiedzi podaj wynik dla wywołania nr 2
anagram.txt fotowoltaika.txt instalacje.txt kraje.txt slowa1.txt slowa2.txt slowa3.txt slowa4.txt urzadzenia.txt r1.jpg r2.jpg r3.jpg r4.jpg
iloczyn(x, y):
jeżeli y = 1:
wynikiem jest x
w przeciwnym razie:
k = y div 2
z = iloczyn(x, k)
jeżeli y mod 2 = 0:
wynikiem jest z + z
w przeciwnym razie:
wynikiem jest x + z + z
Uwaga: x mod y oznacza resztę z dzielenia x przez y, natomiast x div y oznacza wynik dzielenia całkowitego x przez y.
Dla danych liczb x, y interesuje nas liczba wykonywanych operacji dodawania podczas obliczania wyniku funkcji iloczyn(x, y).
Przykład 1.
Dla liczb x=9 i y=11 algorytm wykonuje 5 dodawań. Działanie funkcji iloczyn(9, 11) można zilustrować w następujący sposób (w nawiasach obok wskazano liczbę wykonywanych operacji dodawania):
iloczyn(9, 11) = 9 + z + z, (dwa dodawania) gdzie z = iloczyn(9, 5)
iloczyn(9, 5) = 9 + z + z, (dwa dodawania) gdzie z = iloczyn(9, 2)
iloczyn(9, 2) = z + z, (jedno dodawanie) gdzie z = iloczyn(9, 1)
iloczyn(9, 1) = 9

Uzupełnij poniższą tabelę tak, aby ilustrowała obliczenia wykonywane podczas wywołania iloczyn(10, 45)

W odpowiedzi podaj wynik dla wywołania nr 2